决策树(decision tree)是一个经典的监督学习方法,可以用于解决分类 和回归问题。如下图所示,决策树呈树形结构,它由节点( 若干个内部节 点,用方形表示;若干个叶节点,用圆形表示)和有向边组成。每个内部 节点表示一个属性上的判断,每个分支代表一个判断结果的输出,最后每 个叶节点代表一种分类结果
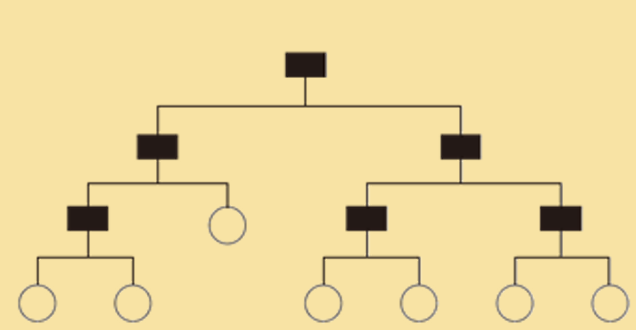
决策树构建过程遵循简单且直观的 “分而治之” (divide-and-conquer)学习策略,
整个决策树生成是基于特征选择策略的递归过程,其返回条件有三种:
① 当前节点包含的样本全属于同一类别,将该节点标记为对应类的叶节点并返回类别;
② 当前属性集为空或是所有样本在所有属性上取值相同,无法划分,标记为叶节点为当
前节点多数样本的类别;
③ 当前节点包含的样本集合为空,不能划分,标记为叶节点,返回父节点样本多类别。
决策树的特征选择即确定最优的属性,我们希望随着划分的进行,决策树的节点所 包含的样本尽可能属于同一类别,这样最终模型判断就越来越明确。通常特征选择的准 则是信息增益(ID3)、增益率(C4.5)或基尼系数(CART)等。
这里我们重点就信息增益展开:
信息熵——>度量样本集合纯度 信息增益——>一次分类后信息熵的减少程度
这里给出公式:
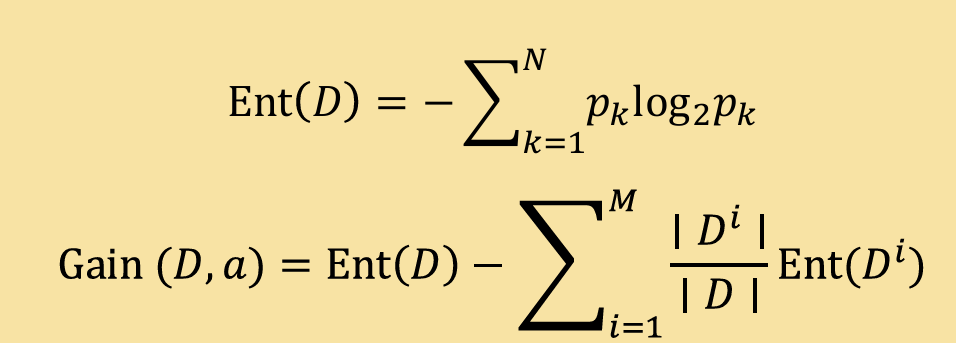
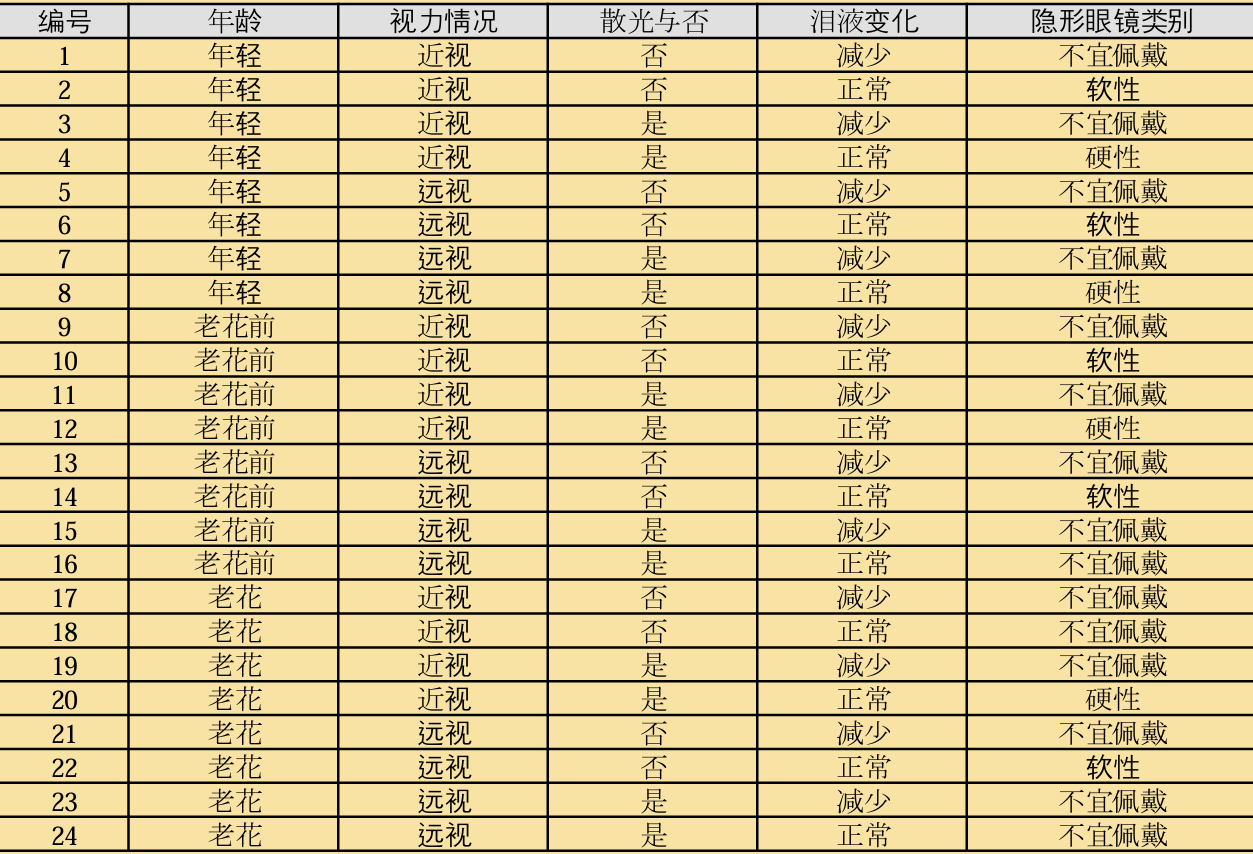
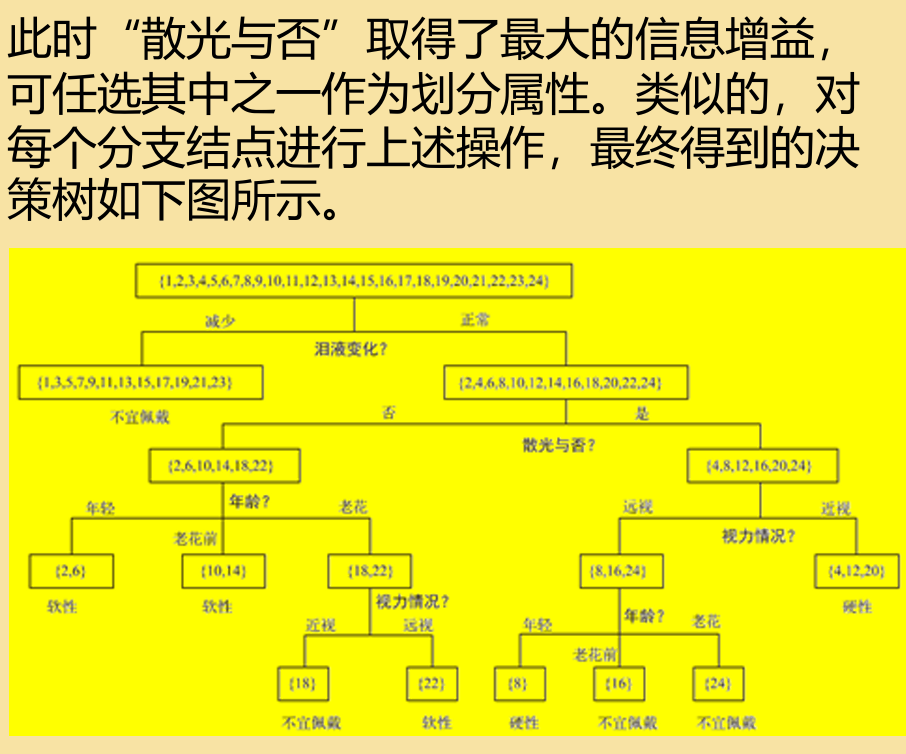
例题:下面表格是一个由24个患 者样本组成的训练数据。样本属 性包括年龄,视力情况,散光与 否以及泪液变化,最后一列是隐 形眼镜类别,接下来请使用信息 增益的特征选择策略来建立一棵 用于推荐隐形眼镜类别的决策树。



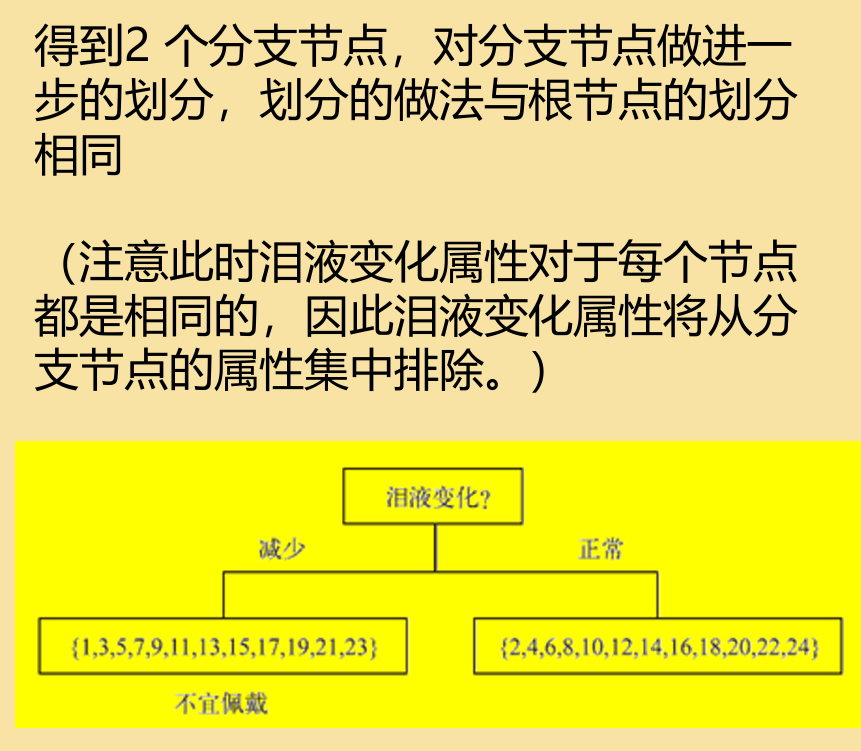

在实际应用中,单个决策树无法有效处理误差等因素,这是我们可以引入一套bagging算法:
Bootstrap Aggregating (Bagging)涉及到创建原始数据集的 多个子集,并在每个子集上训练模型。对最终输出进行平均(用 于回归)或投票(用于分类)。
Bagging 算法可分为以下三个步骤。 •步骤一:给定包含K 个样本的数据集,随机可放回取出K 个样本构成采样集(有 的样本可能没有出现,有的样本可能出现多次),反复进行K 次,产生K 个包含K 个样本的训练集。 •步骤二:每个采样集对应一个训练数据集,训练对应的个体学习器。 •步骤三:将K 个个体学习器结果按相同权重进行取平均( 分类用投票策略,回 归用平均值)
随机森林便是使用Bagging 集成算法的典型算法,个体学习器以决策树变体为模版,在训练过
程中引入了随机属性选择。
传统决策树:
在选择划分属性时是在当前结点的属性集合(假定有d 个属性)中选择一个最优属性;
随机森林:
对个体决策树的每个节点,先从该节点的属性集合中随机选择一个包含k 个属性的子集,然后再选择一个最优属性用于划分。当k=d 时,则完全等价于传统决策树;若k=1 则是随机选择1 个属性用于划分;一般情况下,推荐值k = log (2d )

随机森林的具体过程:
① 使用Bagging 算法构建T 个样本集
② 并行训练T 个决策树。当每个样本有M 个属性时,在决策树的每个节点需要分裂时,随机从这M 个属性中选取出m 个属性,满足条件m << M。然后从这m 个属性中采用某种策略(比如说信息增益)来选择1 个属性作为该节点的分裂属性,一直到不能够再分裂为止。
③ T 个决策树,对应T 个结果(分类是类别结果,回归是数值结果),最终结果通过投票/平均来给出最终随机森林的结果。