引入:感知机面对线性不可分问题的无能

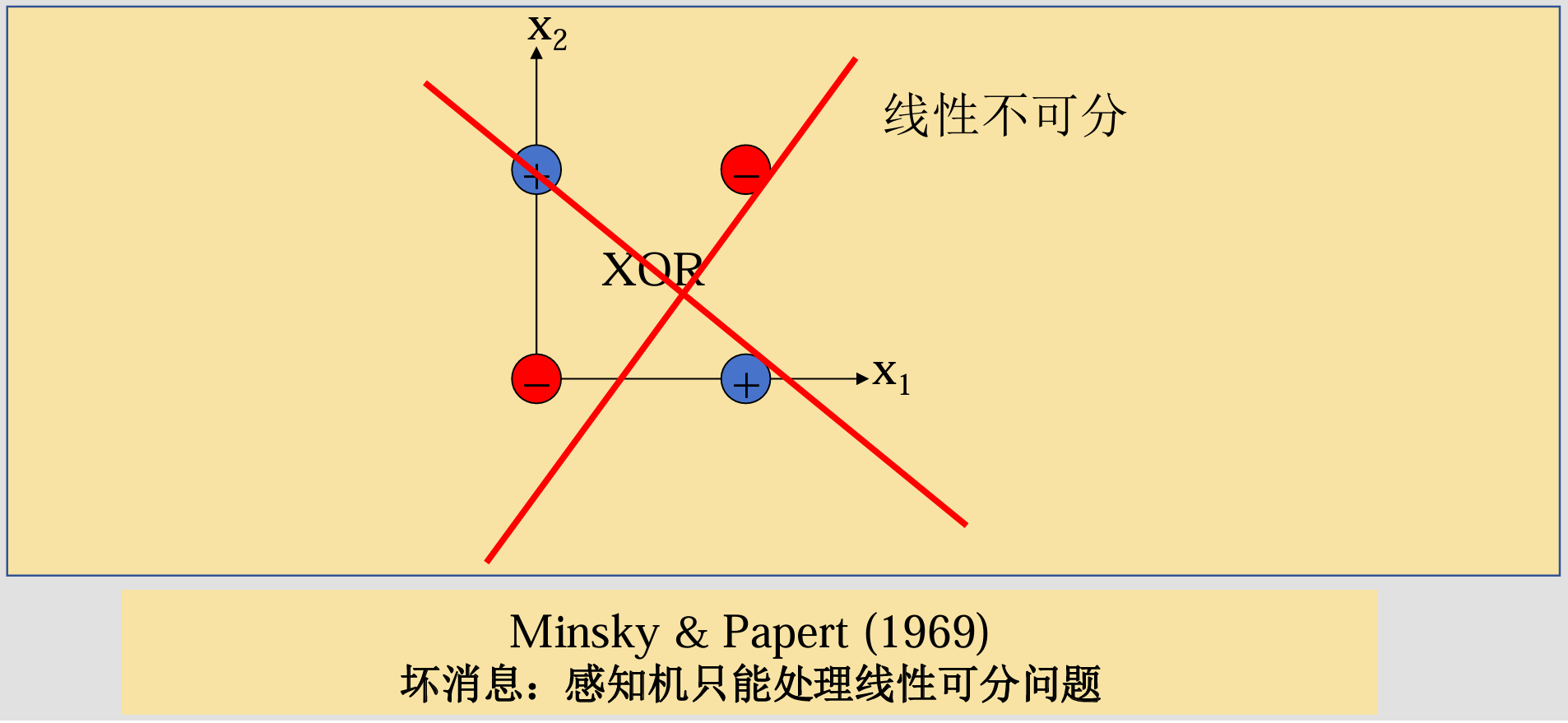
探究:什么是线性不可分问题
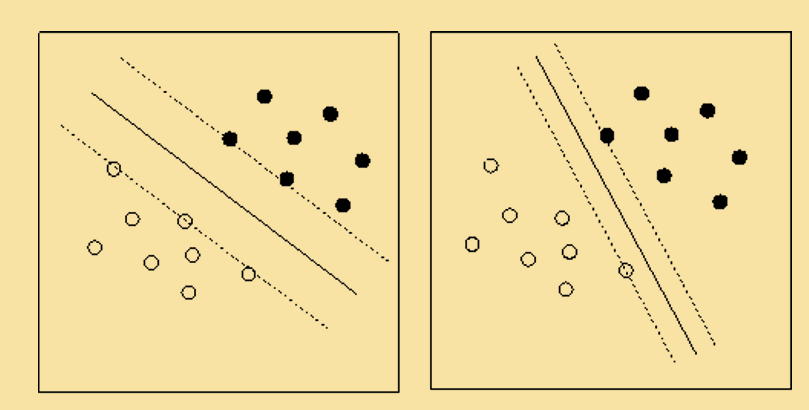
在二维坐标空间中,线性可分问题是指可以用一条直线将两个类别完全分开,如下图所示,其中白色点代表某一种类别的样本,而黑色点代表另一种类别的样本,这两个类别的样本可以由直线完全区分开,即这两个类别是线性可分的。
数学定义:
假设𝐷0和𝐷1是欧氏空间中两个点集,如果存在n 维向量w 和实数b,使得所有属于𝐷0的点𝑥𝑖都有𝜔𝑥𝑖+b > 0,而对于所有属于 𝐷1的点𝑥𝑗则有𝜔𝑥𝑗+b < 0,则称𝐷0和𝐷1线性可分。
以下给出一些关键概念
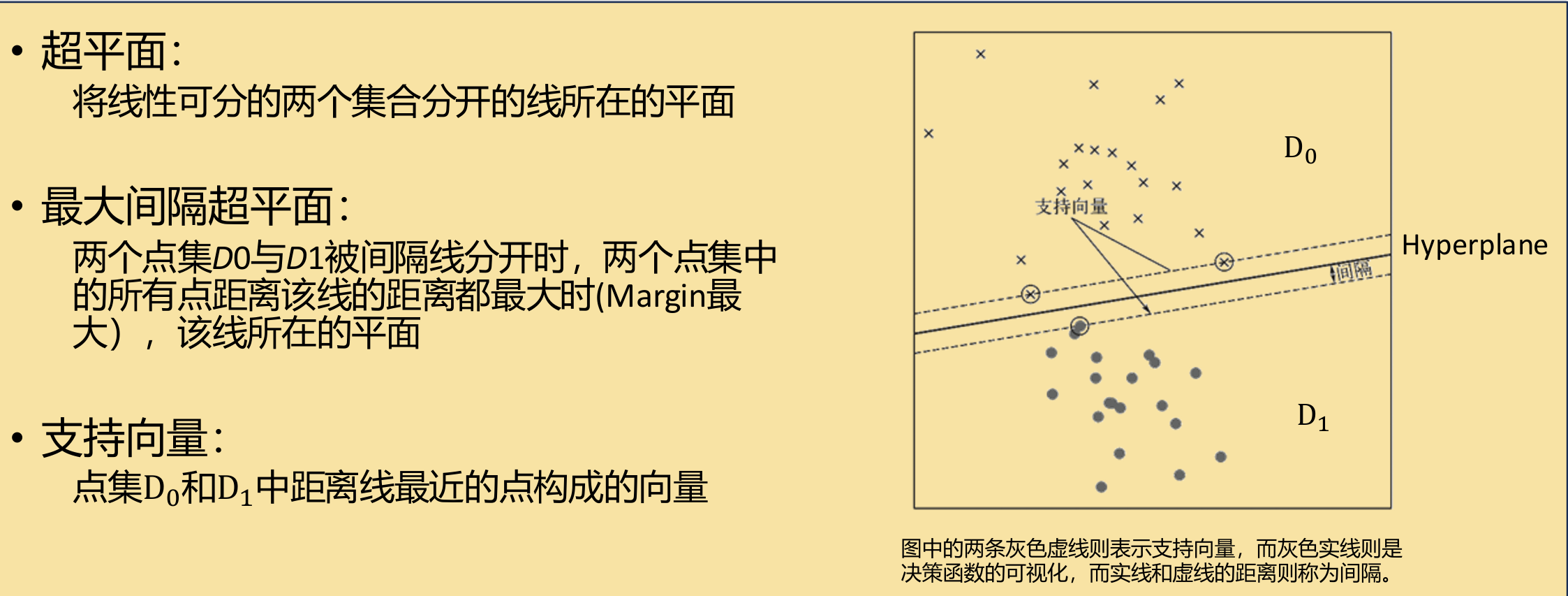
从硬间隔支持向量机入手看线性可分
Firstly,硬间隔支持向量机(Hard Margin Support Vector Machine)是一种严格分离不同类别的数据点而不产生重叠和误分类的支持向量机。
Secondly,硬间隔支持向量机确保了完美的分类分离,但对异常值很敏感,只适用于线性可分的数据。
硬间隔支持向量机的目标是在保证正确分类的同时最大化边际。
有关求最大化边际的方法,相当于把二维空间点到直线距离的思想迁移到到n维空间上,这里给出我手写的笔记:

从软间隔支持向量机入手看线性不可分
Firstly,软间隔支持向量机(Soft Margin Support Vector Machine)是支持向量机的一种变体,它允许一定程度的误分类。
Secondly,该方法对异常值具有较强的鲁棒性,适用于非线性可分数据或有噪声数据。
Thirdly,为了避免误分类,相较于硬间隔SVM引入了松弛变量,即:
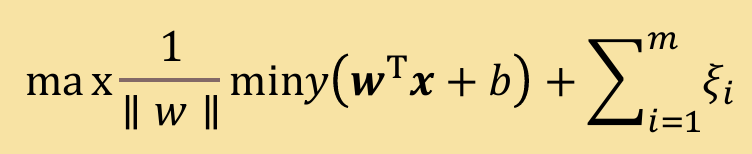
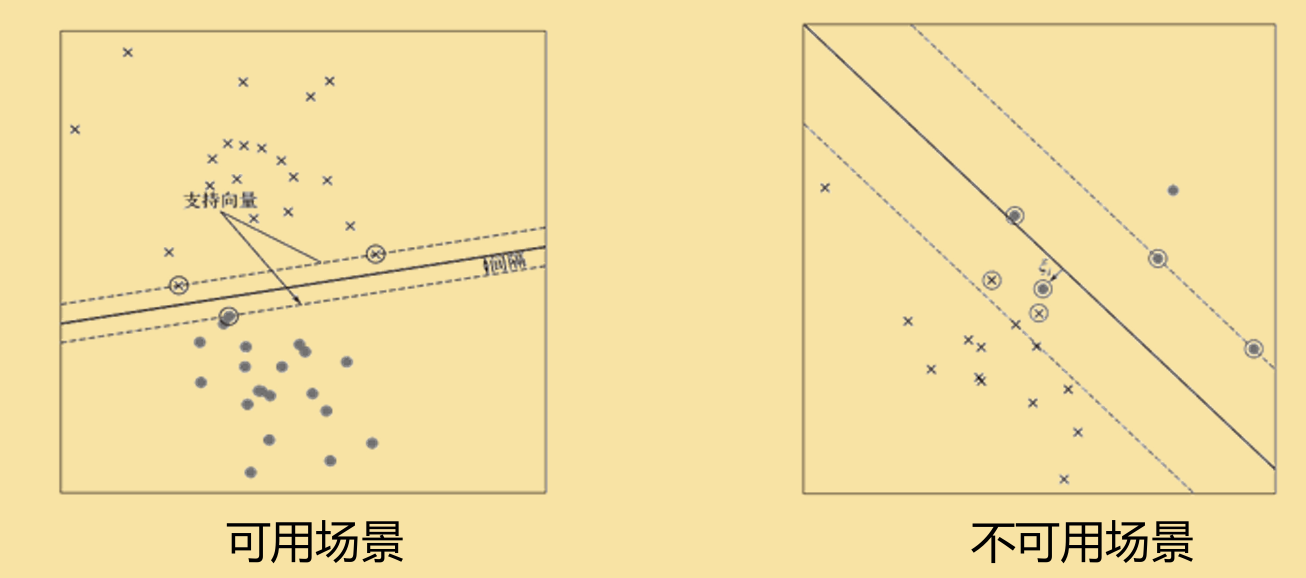
*左图为软间隔SVM,右图为核函数维度升高的模拟

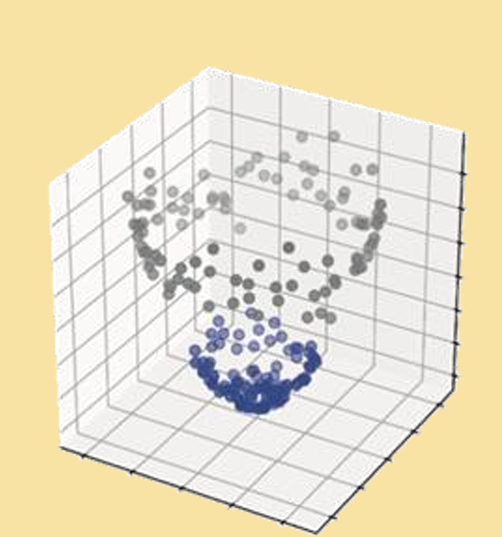
展望:核支持向量机的解决方案
(由于楼主水平有限,本章节仅作初步介绍)
•支持向量机使用核函数将输入数据转换到高维空间。这使得更容易找到分离数 据的超平面。常见类型包括线性、多项式和高斯核函数(径向基核函数)核