美国心理学家 W. McCulloch 和数学家 W. Pitts 基 于生物神经元的特点,在 1943 年在论文 《神经活 动中所蕴含思想的逻辑活动》 首次提出了 McCulloch-Pitts(M-P)人工神经元模型
• M-P 人工神经元模型是一个多输入单输出的信息处理单元;
• 人工神经元的输入可分为兴奋性输入和抑制性输入这两种类型;
• 人工神经元具有空间整合特性和阈值特性;
• 人工神经元输入与输出间有固定的时间延迟;
• 在人工神经元模型设计中通常忽略时间整合作用以及兴奋期后的不应期;
• 人工神经元本身是非时变的,即其突触时延和突触强度均为常数。
以下呈现生物神经元与人工神经元的类比:
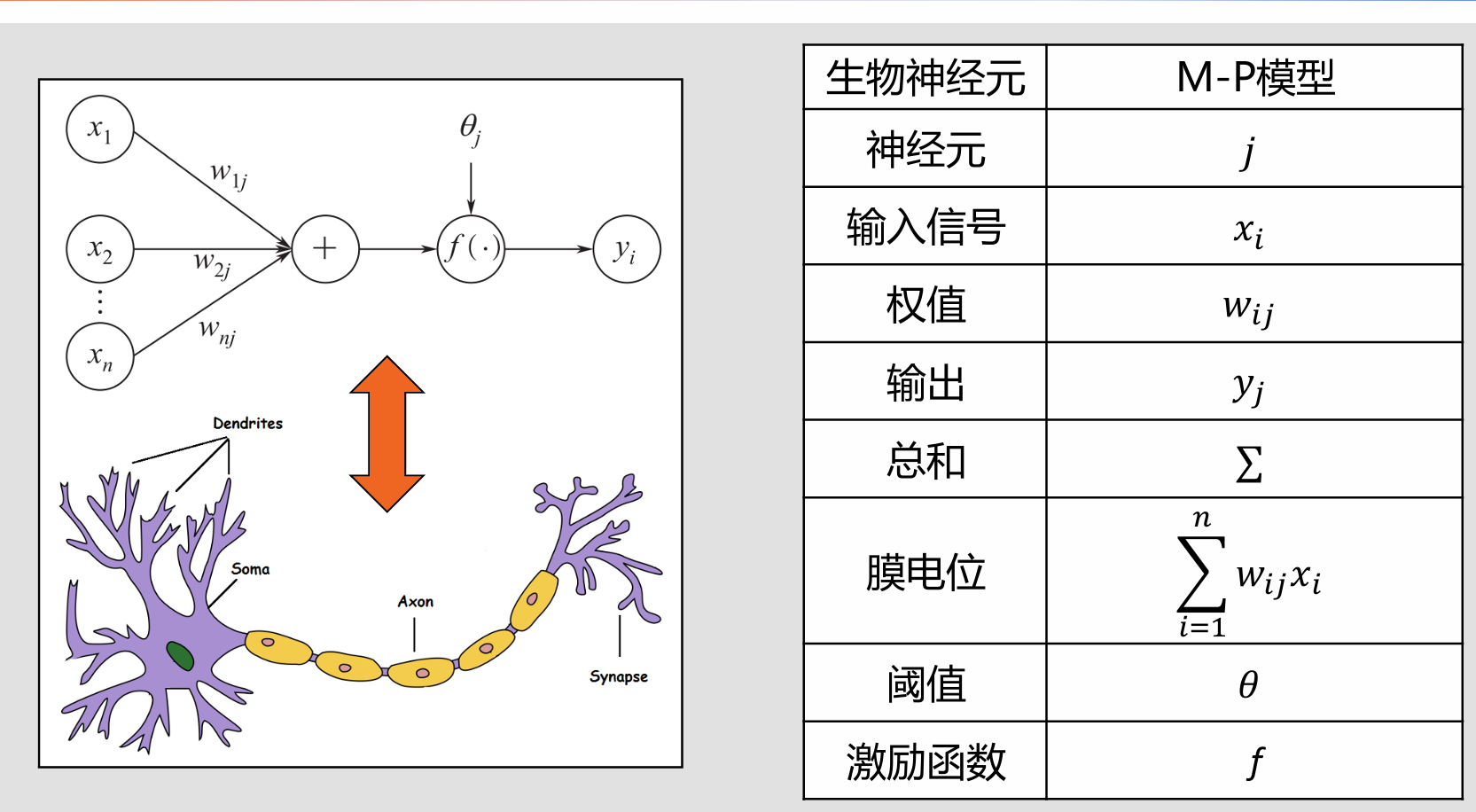
为了方便,接下来涉及如何用MP模型去实现逻辑门的内容将由我的手写笔记组成:

需要指出的是,以上的过程缺乏学习,仅仅是提出这样的一个模型,为了让人工神经元具备学习能力,科学家摸索出了两套方案
无监督学习————Hebb学习规则
w𝑖𝑗(t + 1) = w𝑖𝑗(t) + αy𝑗(t)y𝑖(t)
其中𝛼表示学习率, 𝑤ij(𝑡+1)和𝑤ij(𝑡)分别表示在𝑡+1时刻和𝑡时刻,人工神经元𝑗到人工神经元𝑖的连接强度,而𝑦𝑖和𝑦𝑗为人工神经元𝑖和𝑗的输出。Hebb 学习规则隶属于无监督学习算法的范畴,其主要思想是根据两个人工神经元的激发状态来调整其连接关系,以此实现对简单生物神经活动的模拟
监督学习————Delta学习规则
w𝑖𝑗(t + 1) = w𝑖𝑗(t) + α(d𝑖 - y𝑖)y𝑗(t)
继Hebb 学习规则之后,人工神经元的有监督 Delta 学习规则被提出,用以解决在输入输出已知的情况下神经元权值的学习问题。
其中,𝛼 表示学习率,𝑑𝑖和 𝑦𝑖 为人工神经元 𝑖的期望输出和实际输出, 𝑦𝑗(𝑡)表示人工神经元 𝑗在 𝑡时刻的状态(激活或抑制)。从直观上来说,当人工神经元 𝑖的实际输出比期望输出大,则减小与已激活神经元的连接权重,同时增加与已抑制神经元的连接权重;当人工神经元 𝑖的实际输出比期望输出小,则增加与已激活神经元的连接权重,同时减小与已抑制神经元的连接权重。