交叉熵损失函数定义

我们一般采用经典交叉熵（cross entropy, CE）损失函数来计算模型预测值与真实标签值的误差。交叉熵是信息论中一个重要概念，其作用主要用于度量两个概率分布间的差异性信息。给定一个样本x，p和q为其两个概率分布，通过q表示p的交叉熵，公式如下：

H(p, q) = -p(x) log q(x)

其中，x表示样本，p(x)表示真实概率分布，q(x)表示预测概率分布。

交叉熵刻画了两个概率分布之间的距离，旨在描述通过概率q来表达概率p的困难程度

交叉熵值越小，表明𝑝和𝑞两个概率值越接近。

交叉熵损失计算示例

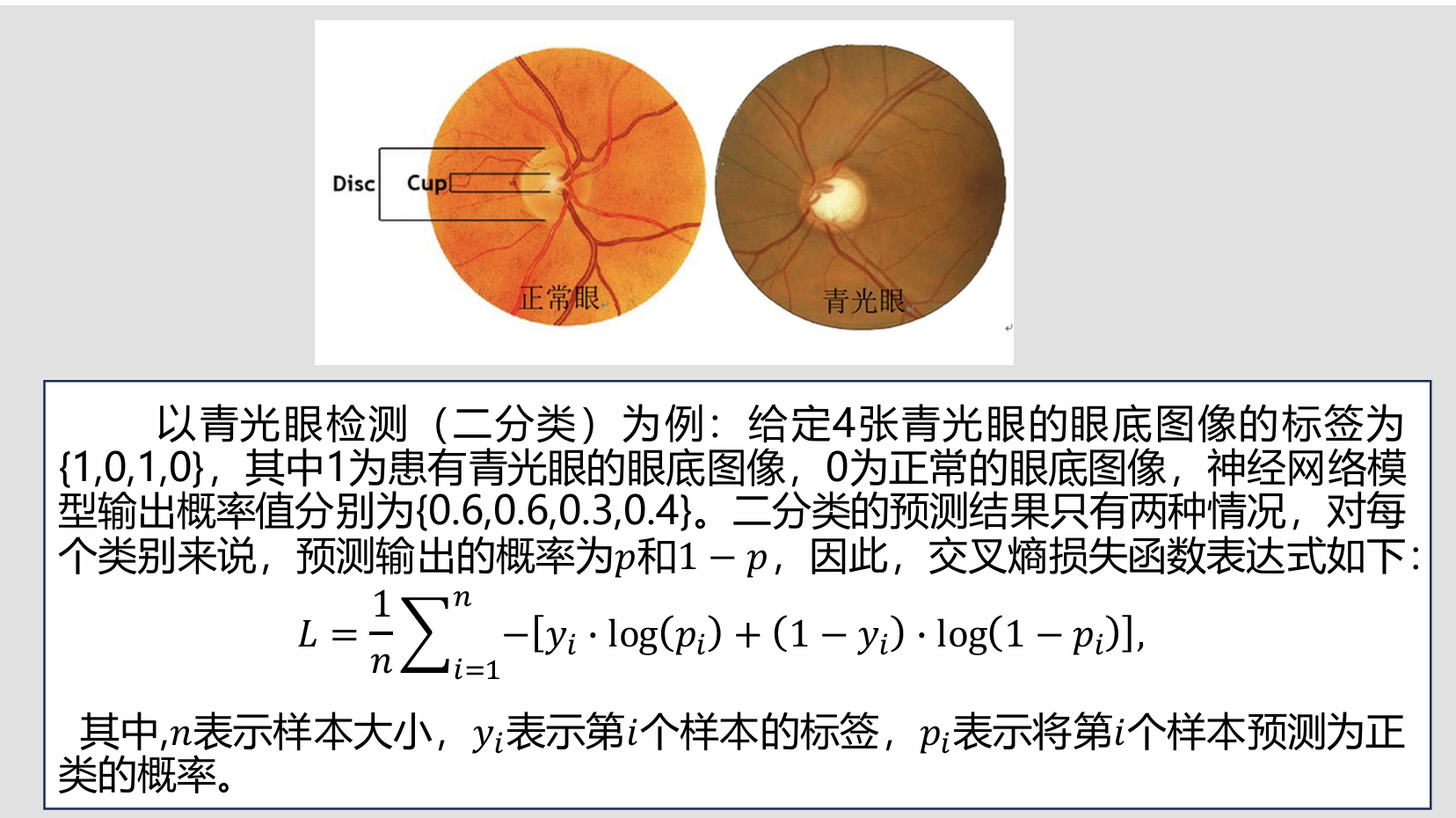
L = -¹/₄[(1×log0.6 + 0×log(1 - 0.6)) + (0×log0.6 + 1×log(1 - 0.6)) + (1×log0.3 + 0×log(1 - 0.3)) + (0×log0.4 + 1×log(1 - 0.4))]

= -¹/₄(log0.6 + log0.4 + log0.3 + log0.6) =......（底数根据需求选择，得到一个结果）

让我们拓展到多分类问题

对于多分类问题，假设训练集中有n个样本，样本的真实标签y和预测概率分布p的交叉熵损失如下：

L = ¹/_n Σⁿ_i=1 CrossEntropy(y⁽ⁱ⁾, ŷ⁽ⁱ⁾)

其中，CrossEntropy(y⁽ⁱ⁾, ŷ⁽ⁱ⁾) = -Σ^C_j=1 y_j⁽ⁱ⁾ log ŷ_j⁽ⁱ⁾

由于元素y的取值只有0或1，从交叉熵的表示形式可以看出，交叉熵只关注样本真实类别的新概率。 而对于二分类问题，L = -¹/_n Σⁿ_i=1 [-y_i log p_i + (1 - y_i) log (1 - p_i)]

其中，n表示样本大小，y_i表示第i个样本的标签，p_i表示第i个样本预测结果。