1. 张量的基本定义
在计算机图像处理中，张量(Tensor)是一种多维数组结构，用于高效表示和操作图像数据及其他高维数据。
数学背景：张量是向量和矩阵的高维推广，可视为多维数组。其"阶"(或"秩")表示维数：
- 0阶张量：标量(单个数值)
- 1阶张量：向量(一维数组)
- 2阶张量：矩阵(二维数组)
- 更高阶：三维及以上数组(如RGB图像、视频序列等)
图像处理中的张量：通常指3阶或4阶张量，用于表示批量的图像数据。
基础篇：
张量与维度
2. 图像处理中的张量表示
(1) 单张图像
- 灰度图像：2阶张量(高度 × 宽度)
- RGB彩色图像：3阶张量(高度 × 宽度 × 通道数)，例如 (256, 256, 3)
(2) 批量图像
- 深度学习批量处理彩色图像：4阶张量(高度 × 宽度 × 通道数 × 批次，这里的批次指样本数量)
- 短视频：4阶张量(高度 × 宽度 × 通道数 × 批次，这里的批次指帧数)
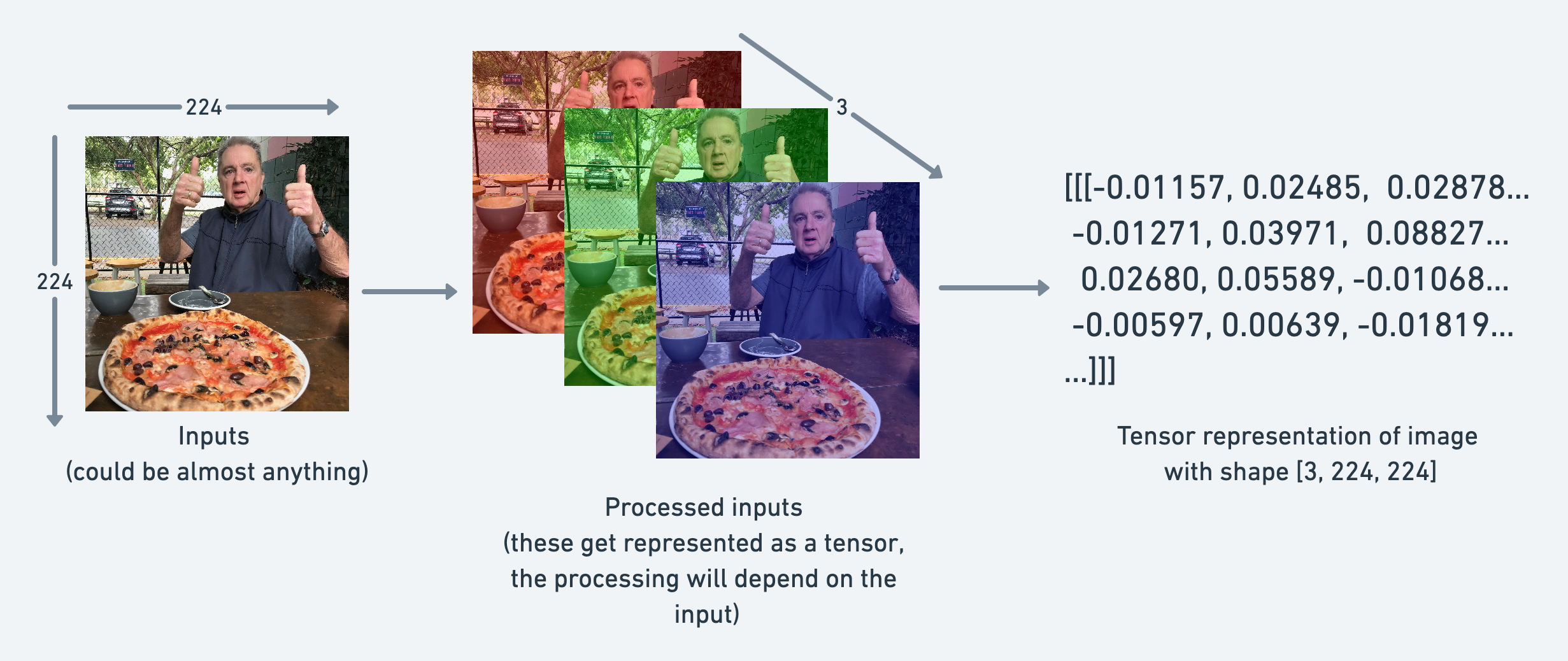
*5阶张量则出现于深度学习批量处理短视频或长视频（由4阶的视频片段组成）中
3. 为什么使用张量？
- 统一数据结构：张量能整合图像、批量数据、多通道信息，便于并行计算(如GPU加速)
- 深度学习框架支持：TensorFlow、PyTorch等库的核心数据结构均为张量，支持自动微分和优化
- 高维操作：方便实现卷积、池化等图像处理操作
3. 主流框架下张量写法
*C表示通道数，H表示高度，W表示宽度，N表示个数
- Pytorch：(N, C, H, W)，通道优先
- Tensorflow：(N, H, W, C)，通道最后