如果你看过3blue1brown讲解有关线性代数的视频,你一定对矩阵运算有了更为深刻的认识。 矩阵乘法的本质是对既有图形进行线性变换。如果是一个行列式不为0的方阵去乘,图形将在同一维度 下进行拉伸、旋转等操作,而如果是行列式为0的方阵去乘,相当于过度压缩以至于发生降维(如把一个正方形挤压 成一条线),如果是非方阵的矩阵去乘,则涉及到直接的维度转换。
图像呈现在计算机屏幕上,是典型的二维空间,因此谈到图像处理,自然离不开有关线性代数知识的参与,下面的图片来自 David.C.Lay所编写的线性代数教材,呈现了对称、收缩、拉伸、剪切、投影变换的矩阵乘法实现。
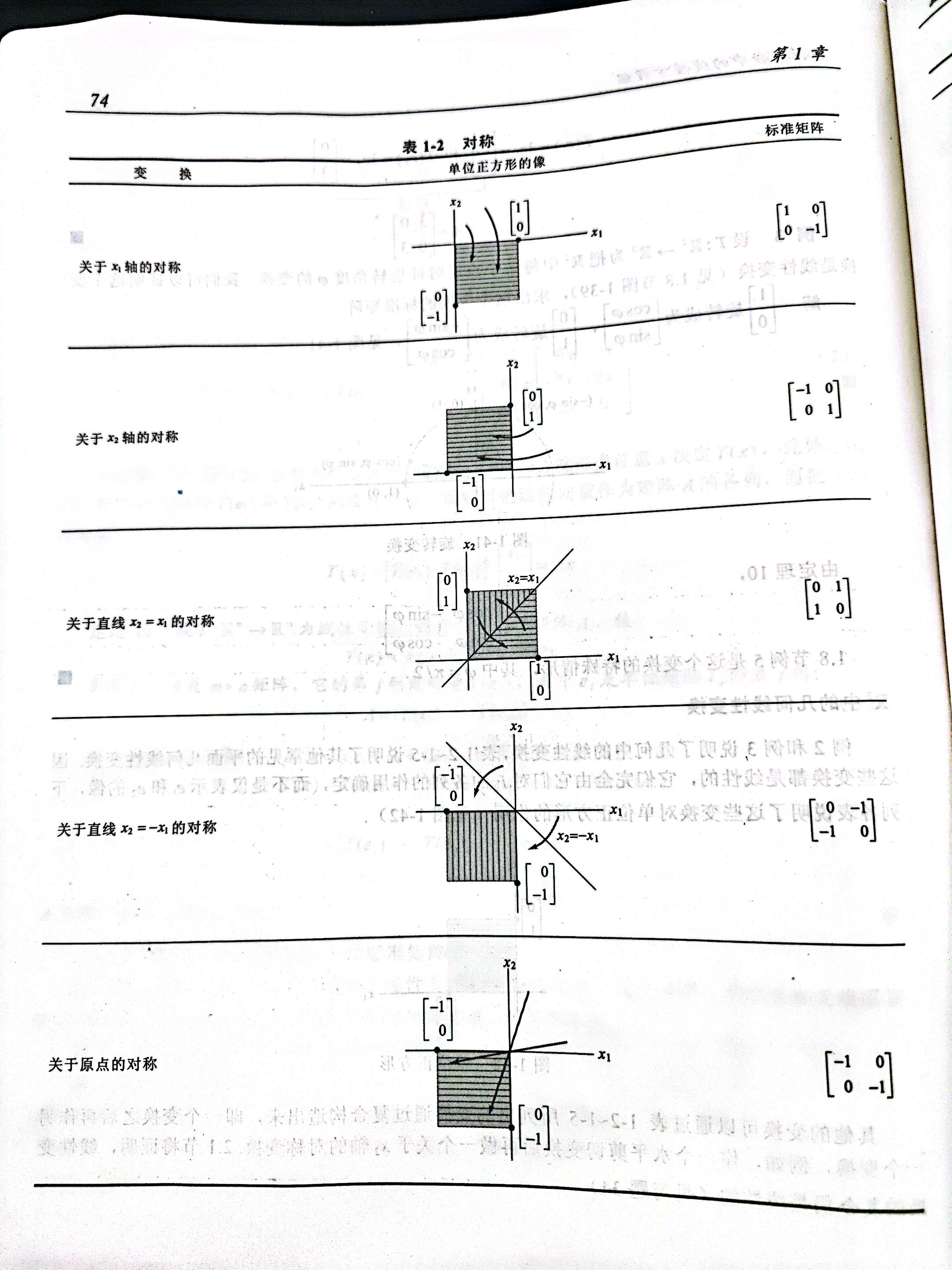
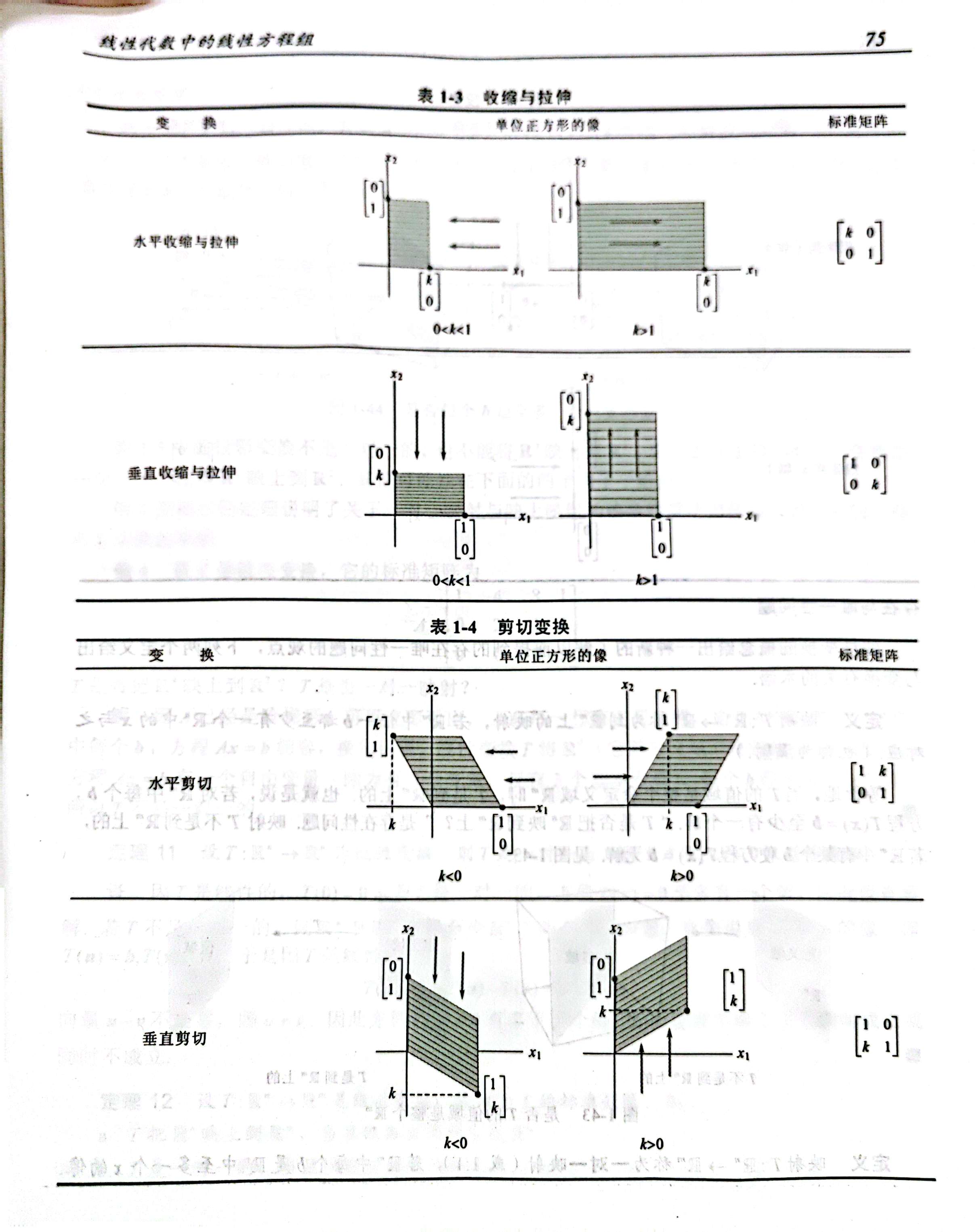
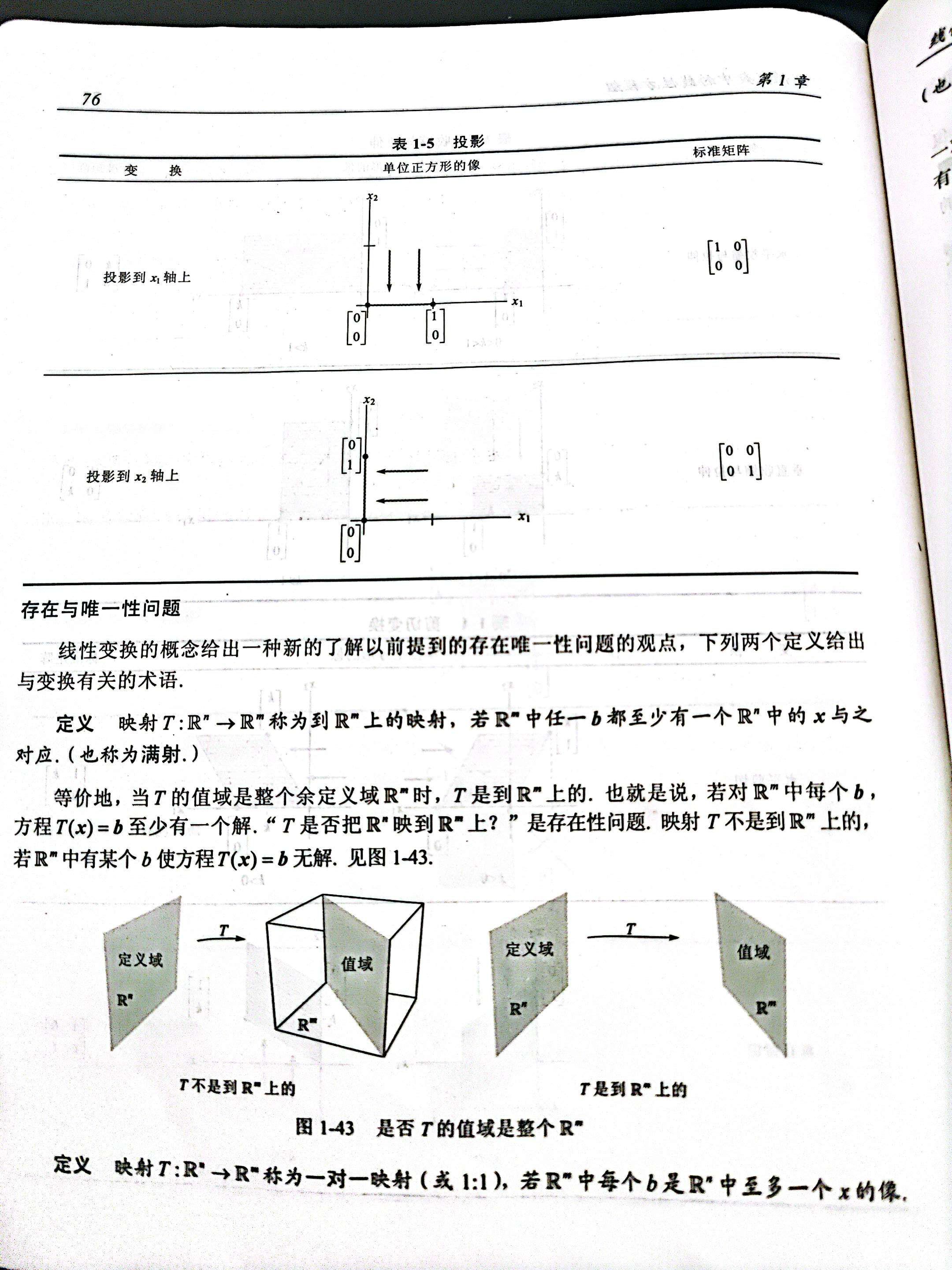
下面是在知乎上找到的旋转变换的矩阵实现
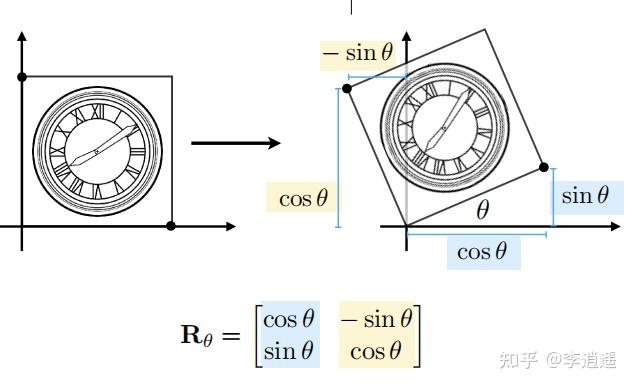
这样看,只要我们去乘一个二维方阵,似乎就能解决一切图像处理问题
很遗憾地告诉你,二维的矩阵乘法无法解决所有二维空间的几何转换,如平移

为了解决像平移这样特殊的几何变换,我们需要引入一个全新的概念——齐次坐标
齐次坐标是一种将二维坐标扩展到三维空间的方法,它通过在原始坐标的基础上添加一个额外的维度来实现。 在二维空间中,我们通常使用(x, y)来表示一个点的坐标。而在齐次坐标中,我们使用(x, y, w)来表示一个点的坐标,其中w表示点的权重。
说通俗一点,我们进行了升维操作

你肯定会很奇怪,平面里的平移放在一个空间里不还是平移吗,为什么这个时候就可以使用矩阵乘法完成线性变换了呢,其实,二维空间的平移放到三维空间里相当于剪切操作
不要着急,我们先类比二维空间,当我们剪切一个正方形时,正方形变成平行四边形,组成正方形的 一维线段发生了平移。发现了吗?当我们对低维空间做平移或者是别的难以处理的仿射变换的时候, 放在高维空间里就能转化为简单的线性变换。是不是很神奇!
下面给出python的代码演示,在你的IDE上运行这些代码,你将对这些变换有着更加直观的认识:
import numpy as np
import matplotlib.pyplot as plt
# 定义一个简单的矩形作为初始几何对象
def create_rectangle():
return np.array([
[0, 0, 1], # 使用齐次坐标 (x, y, w)
[2, 0, 1],
[2, 2, 1],
[0, 2, 1],
[0, 0, 1] # 回到起点闭合矩形
])
# 对称变换(关于 y 轴反射)
def symmetry_matrix():
return np.array([
[-1, 0, 0], # x 轴取反,y 不变
[0, 1, 0],
[0, 0, 1]
])
# 收缩变换(均匀缩小)
def contraction_matrix(scale=0.5):
return np.array([
[scale, 0, 0],
[0, scale, 0],
[0, 0, 1]
])
# 拉伸变换(x 轴拉伸)
def stretch_matrix(sx=2.0):
return np.array([
[sx, 0, 0],
[0, 1, 0],
[0, 0, 1]
])
# 剪切变换(沿 x 轴剪切)
def shear_matrix(shear_x=0.5):
return np.array([
[1, shear_x, 0],
[0, 1, 0],
[0, 0, 1]
])
# 投影变换(透视投影模拟,假设 z=1 平面投影到 y=0)
def projection_matrix():
return np.array([
[1, 0, 0], # 投影到 y=0,保留 x
[0, 0, 0], # y 变为 0
[0, 0, 1]
])
# 平移变换
def translation_matrix(tx=1, ty=1):
return np.array([
[1, 0, tx],
[0, 1, ty],
[0, 0, 1]
])
# 旋转变换(逆时针旋转,角度单位为度)
def rotation_matrix(angle_deg=45):
theta = np.radians(angle_deg) # 转换为弧度
cos_theta = np.cos(theta)
sin_theta = np.sin(theta)
return np.array([
[cos_theta, -sin_theta, 0],
[sin_theta, cos_theta, 0],
[0, 0, 1]
])
# 应用变换
def apply_transformation(points, matrix):
return points @ matrix.T # 矩阵乘法,注意转置以匹配维度
# 绘制几何对象
def plot_shape(points, title):
plt.plot(points[:, 0], points[:, 1], 'b-', label=title)
plt.title(title)
plt.axis('equal') # 保持比例
plt.grid(True)
plt.legend()
plt.show()
# 主程序
def main():
# 创建初始矩形
original_shape = create_rectangle()
# 定义所有变换
transformations = [
("Symmetry (Reflection about Y-axis)", symmetry_matrix()),
("Contraction (Scale = 0.5)", contraction_matrix(0.5)),
("Stretch (X-axis Stretch = 2)", stretch_matrix(2.0)),
("Shear (X-axis Shear = 0.5)", shear_matrix(0.5)),
("Projection (to Y=0)", projection_matrix()),
("Translation (tx=1, ty=1)", translation_matrix(1, 1)),
("Rotation (45 degrees)", rotation_matrix(45))
]
# 绘制原始图形
plot_shape(original_shape, "Original Shape")
# 每个变换独立作用于原始图形并绘制
for title, matrix in transformations:
transformed_shape = apply_transformation(original_shape, matrix)
plot_shape(transformed_shape, title)
if __name__ == "__main__":
main()
三维空间什么时候需要升维到四维空间去处理呢?这里偷个懒,直接搬运了David.C.Lay教材上透视投影的内容,不做多余说明:
